Problema 36

Demostrar que $ \lim_{\theta\to0}\frac{\sin\theta}{\theta} = 1 $

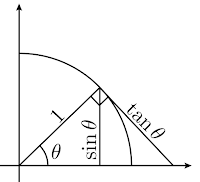
Demostración. Obsérvese la figura que acompaña la demostración. En la figura se ilustra la definición de $\sin\theta$ y $\tan\theta$ en la circunferencia unitaria. Más aún, como el radio es 1, el arco que subtiende al ángulo $\theta$ mide $\theta$. Suponiendo que $0 < \theta < \frac{\pi}{2}$ se cumple que

$$ \sin\theta < \theta < \tan\theta $$

Notando que $\frac{\sin\theta}{\theta} > 0$ y $\theta$ se sigue que

$$ \frac{1}{\sin\theta}>\frac{1}{\theta} > \frac{1}{\tan\theta} $$ $$ \frac{\theta}{\sin\theta} > 1 > \frac{\theta}{\tan\theta} $$ $$ \frac{\theta}{\sin\theta} > 1 > \frac{\theta\cdot\cos\theta}{\sin\theta} $$ $$ \frac{\theta}{\sin\theta} \frac{\sin\theta}{\theta} > 1 \cdot \frac{\sin\theta}{\theta} > \frac{ \theta \cdot \cos \theta}{ \sin \theta} \frac{\sin\theta}{\theta} $$ $$ \cos\theta < \frac{\sin\theta}{\theta} < 1 $$

Además, como el seno es una función impar y el coseno es una función par se tiene que $\frac{\sin\theta}{\theta} = \frac{\sin(-\theta)}{-\theta}$ y $\cos\theta=\cos(-\theta)$, la misma desigualdad se cumple para $\theta < 0$. Esto último nos permite tomar el límite $\theta\to 0$ sin necesidad de hacerlo por la derecha. Así,

$$ \lim_{\theta\to 0} \cos\theta \leq\lim_{\theta\to 0} \frac{\sin\theta}{\theta} \leq \lim_{\theta\to 0}1 $$

Notando que $\displaystyle \lim_{\theta\to 0}\cos\theta=1$, por el teorema del sándwich se tiene que $$ \lim_{\theta\to 0}\frac{\sin\theta}{\theta} = 1 \qquad \blacksquare $$