Límites

Introducción

La herramienta fundamental para el análisis del comportamiento de funciones es el límite.

Particularmente, se dice que una función \(f\) tiene un límite \(L\) en \(c\) si en las proximidades de \(c\) los valores \(f(x)\) se acercan arbitrariamente a \(L\). Esto se denota

Que se lee "el límite de \(f\) cuando \(x\) tiende a \(c\)". Esto quiere decir que los valores de \(f(x)\) se acercan a \(L\) tanto como se desee haciendo que \(x\) diste lo suficiente de \(c\).

Intuitivamente (e incorrectamente), para funciones que se portan bien, bastará con corroborar que \(f(c)=L\) para comprobar que los valores del contradominio bailan cerca de \(L\) cuando los valores del dominio bailan cerca de \(c\).

Definición \( \varepsilon - \delta \) del límite

La noción de "acercarse" conlleva inherentemente el concepto de "cercanía", que claramente no está definido. ¿Qué tan cerca es cerca? Pues bien, para evitar ambigüedades, es tanto como uno quiera. De esta idea y de la definición informal de la sección anterior se tiene la definición.

Definición. Se denota por \(\displaystyle\lim_{x\to a}f(x)\) al límite en \(a\) de una función \(f\), y $$ \lim_{x\to a}f(x) = L \iff \forall \varepsilon > 0 \, \exists \delta > 0:\; 0 < |x-a| < \delta \implies |f(x)-L| < \varepsilon $$

Esta definición retoma la idea de "acercamiento" a \(a\) sin la necesidad de evaluar la función en ese punto, por lo que solamente se tratan los valores en una vecindad de \(a\).

La definición estipula que, sin importar qué tan cerca se desea estar de \(L\) (a esta distancia se le llama \(\varepsilon\)), siempre es posible acercarse lo suficiente a \(a\) (tanto como \(\delta\)) para que los valores \(f(x)\) se acerquen a \(L\) tanto como se deseaba.

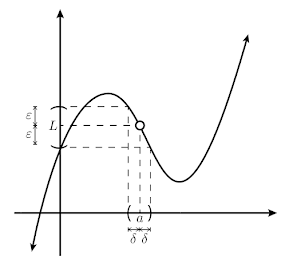
Recuperando los ejemplos anteriores,

Podemos definir una suerte de receta (que para nada pretende ser un algoritmo de demostración que sea correcto en todos los casos) para poder guiar estas demostraciones:

1. Identificar \(|x-a|\).
2. Evaluar \(|f(x)-L|\).
3. Simplificar la expresión hasta encontrar algo de la forma \(\alpha|x-a|\)
4. Hacer \(\delta=\frac{\varepsilon}{\alpha}\) y demostrar el límite.

En dado caso que se desee demostrar la inexistencia de un límite en algún punto determinado, se debe demostrar que la negación de la definición se cumple en ese punto, i.e. $$ \exists \varepsilon \; \forall \delta: \, 0 < |x-a| < \delta\land |f(x)-L| > \varepsilon $$

Ejemplo. Demostrar que \(\displaystyle\lim_{x\to 0}\frac{1}{x}\) no existe.

Demostración. Se demostrará que, para cualquier valor \(L\), $$ \exists \varepsilon \; \forall \delta: \,0 < |x-0| < \delta \land \left|\frac{1}{x}-L\right| > \varepsilon $$ Sea \(|x| < \delta\), de donde \(\frac{1}{|x|}>\frac{1}{\delta}\). Así, \(\left|\frac{1}{x}\right| > \frac{1}{\delta}\), por lo que $$ \frac{1}{\delta} < \left|\frac{1}{x}-L+L\right|\leq \left|\frac{1}{x}-L\right|+\left| L\right| $$ Así, \(\left|\frac{1}{x}-L\right| > \frac{1}{\delta}-|L|\). Sea \(\varepsilon=\left|\frac{1}{x}-L\right|\). Se tiene entonces que \(\forall\delta\) se cumple \(0 < |x-0| < \delta\) y \(\left|\frac{1}{x}-L\right| > \varepsilon\)

Obsérvese que la definición de límite no ofrece un método de cálculo de límites: el valor del límite ya se encontraba propuesto en todos los ejemplos vistos. La siguiente sección ofrece algunos teoremas de gran utilidad para el cálculo de límites, y la sección subsecuente contiene una gran cantidad de ejemplos.

Teoremas de límites

Teorema de unicidad del límite. Si \(\displaystyle\lim_{x\to a}f(x)=L\) y \(\displaystyle\lim_{x\to a}f(x)=M\), entonces \(L=M\).

Demostración. Por hipótesis, \(\forall\varepsilon\;\exists\delta_1,\delta_2:\)

1. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)
2. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)

Teorema. Si \(\displaystyle\lim_{x\to a}f(x)=L\) y \(\displaystyle\lim_{x\to a}g(x)=M\), entonces

1. \(\displaystyle\lim_{x\to a}(f+g)(x)=L+M\)
2. \(\displaystyle\lim_{x\to a}(f\cdot g)(x)=L\cdot M\)
3. Y si \(M\not = 0\), \(\displaystyle\lim_{x\to a}\left(\frac{f}{g}\right)(x)=\frac{L}{M}\)

P.D. $$ \forall\varepsilon>0\;\exists\delta > 0:\, 0 < |x-a| < \delta \implies |(f+g)(x)-(L+M)| < \varepsilon $$

Demostración. Por hipótesis, \(\forall\varepsilon\;\exists\delta_1,\delta_2:\)

1. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)
2. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)

P.D. $$ \forall\varepsilon > 0 \; \exists \delta>0:\, 0 < |x-a| < \delta \implies |(f\cdot g)(x)-(L\cdot M)| < \varepsilon$$

Demostración. Por hipótesis, \(\forall\varepsilon\;\exists\delta_1,\delta_2:\)

1. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)
2. \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2}\)

Observación. $$ \begin{align} |(f\cdot g)(x)-L\cdot M| & = |f(x)g(x)-M\cdot f(x)+M\cdot f(x)-L\cdot M|\\ & = |f(x)(g(x)-M) + M(f(x)-L)|\\ & \leq |f(x)|\,|g(x)-M|+|M|\,|f(x)-L| \end{align} $$ Por lo que bastará mostrar que esto último es menor que \(\varepsilon\). Sin pérdida de generalidad, sea \(\varepsilon_1 \leq 1\), por lo que \(|f(x)|-|L| < |f(x)-L| < 1\), de donde \(|f(x)| < 1+|L|\). Así, bastará probar que $$ (1+|L|)|g(x)-M|+(1+|M|)|f(x)-L| < \varepsilon $$ Y se pueden hallar \(\delta_1,\delta_2\) tales que \(0 < |x-a| < \delta_1\implies |f(x)-L| < \frac{\varepsilon}{2(|M|+1)}\) y \(0 < |x-a| < \delta_2\implies |g(x)-M| < \frac{\varepsilon}{2(|L|+1)}\) De ahí, $$ \begin{align}|(f\cdot g)(x)-L\cdot M| & < (|L|+1)|g(x)-M|+(|M|+1)|f(x)-L|\\ & < (|L|+1)\frac{\varepsilon}{2(|L|+1)}+(|M|+1)\frac{\varepsilon}{2(|M|+1)}\\ & < \frac{\varepsilon}{2}+\frac{\varepsilon}{2}\\ & < \varepsilon \end{align} $$

Lema \(\displaystyle\lim_{x\to a}\frac{1}{g(x)}=\frac{1}{M}\)

Demostración. Por demostrar que $$ \forall\varepsilon > 0\;\exists\delta > 0:\, 0 < |x-a| < \delta \implies |\frac{1}{g(x)}-\frac{1}{M}| < \varepsilon $$ Obsérvese que $$ \left|\frac{1}{g(x)}-\frac{1}{M}\right| =\left|\frac{M-g(x)}{Mg(x)}\right| = \frac{|g(x)-M|}{|M|\,|g(x)|} $$ Bastará con probar que esto último es menor que \(\varepsilon\). Como \(\displaystyle\lim_{x\to a}g(x)=M\), se tiene que \(\forall\varepsilon > 0\; \exists\delta>0:\, 0 < |x-a| < \delta \implies |g(x)-M| < \varepsilon\). En particular, para \(\varepsilon_1=\frac{|M|}{2}\) hay una \(\delta^*\) tal que \(|g(x)-M| < \frac{|M|}{2}\).

Nótese que \(|M|=|M-g(x)+g(x)|\leq |M-g(x)|+|g(x)|\), de donde \(|g(x)|\leq \frac{|M|}{2}\) y \(\frac{1}{|g(x)|} < \frac{2}{|M|}\) en tanto \(0 < |x-a| < \delta^*\). Por consiguiente, $$ \frac{1}{|M|\,|g(x)|} < \frac{2}{|M|}\cdot\frac{1}{|M|} < \frac{2}{M^2} $$ Sea \(\delta' > 0\) tal que \(|g(x)-M| < \frac{M^2\varepsilon}{2}\). Sea \(\delta = \min\{\delta^*,\delta'\}\) y \(0 < |x-a| < \delta\). Así, $$ \left|\frac{1}{g(x)} - \frac{1}{M}\right|=\frac{|g(x)-M|}{|M|\,|g(x)|} < \frac{2}{M^2}\cdot\frac{M^2}{2}\cdot\varepsilon = \varepsilon $$ Que concluye el lema. \(\blacksquare\)

Para demostrar el inciso 3 basta con aplicar el inciso 2 y el lema, pues $$ \lim_{x\to a}\frac{f(x)}{g(x)}=\lim_{x\to a}f(x)\cdot\frac{1}{g(x)}=\lim_{x\to a}f(x)\cdot\lim_{x\to a} \frac{1}{g(x)}=L\cdot\frac{1}{M} =\frac{L}{M} $$

Cálculo de límites

El cálculo de límites es un proceso informal mediante el cual se proponen valores para un límite y, posteriormente, demostrarlo. No obstante, una vez conocidos los valores de ciertos límites se pueden utilizar los teoremas de la sección anterior para realizar cálculos de límites que son absolutamente formales y no requieren de más demostración que el cálculo mismo. Demostraremos en esta sección el valor de algunos límites que nos ayudarán en futuros cálculos.

Afirmación. \(\displaystyle\lim_{x\to a}x = a\).

Demostración. Sea \(\delta = \varepsilon\). Así, dado \(\varepsilon>0\), si \(|x-a| < \delta\) se sigue que \(|x-a| < \varepsilon\), que es lo que se quería demostrar. \(\blacksquare\)

Afirmación. Sea \(c\in\mathbb{R}\) una constante. \(\displaystyle\lim_{x\to a}c = c\).

Demsotración. El valor de \(\delta\) es indistinto, pues dado \(\varepsilon>0\), si \(|x-a| < \delta\) se sigue que \(|c-c|=0 < \varepsilon\), pues por hipótesis se tiene \(\varepsilon > 0\), que es lo que se quería demostrar. \(\blacksquare\)

Por estas dos afirmaciones y el último teorema de la sección anterior, se sigue que cualquier función polinomial \(f\) dada por \(f(x)=a_0+a_1 x +...+ a_n x^n\) cumple con \(\displaystyle\lim_{x\to a}f(x)=f(a)\). Más aun,

Corolario. Una función \(f\) dada por \(f(x)=\frac{a_0+a_1 x +...+ a_n x^n}{b_0+b_1 x+...+b_m x^m}\) con \(n,m\in\mathbb{N}\) cumple con \(\displaystyle\lim_{x\to a}f(x)=f(a)\) siempre que \(b_0+b_1 a+...+b_m a^m\not = 0\).

En la tarea número 2 se demuestra que la raíz cuadrada cumple con esta misma propiedad.

Procederemos a calcular múltiples límites de funciones racionales y raíces.

Ahora realizaremos un pequeño estudio de límites trigonométricos. Primero enunciaremos y demostraremos geométricamente un teorema fundamental para los límites trigonométricos.

Teorema. \(\displaystyle\lim_{\theta\to0}\frac{\sin\theta}{\theta}=1\)

Demostración. Obsérvese la figura que acompaña la demostración. En la figura se ilustra la definición de \(\sin\theta\) y \(\tan\theta\) en la circunferencia unitaria. Más aún, como el radio es 1, el arco que subtiende al ángulo \(\theta\) mide \(\theta\). Suponiendo que \(0 < \theta < \frac{\pi}{2}\) se cumple que $$ \sin \theta < \theta < \tan\theta $$ Notando que \(\frac{\sin\theta}{\theta}>0\) y \(\theta\) se sigue que $$ \frac{1}{\sin\theta} > \frac{1}{\theta} > \frac{1}{\tan\theta} $$ $$ \frac{\theta}{\sin\theta} > 1 > \frac{\theta}{\tan\theta} $$ $$ \frac{\theta}{\sin\theta} > 1 > \frac{\theta\cdot\cos\theta}{\sin\theta} $$ $$ \frac{\theta}{\sin\theta} \frac{\sin\theta}{\theta} > 1 \cdot \frac{\sin\theta}{\theta} > \frac{\theta\cdot\cos\theta}{\sin\theta} \frac{\sin\theta}{\theta} $$ $$ \cos\theta < \frac{\sin\theta}{\theta} < 1 $$

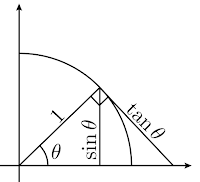
Además, como el seno es una función impar y el coseno es una función par se tiene que \(\frac{\sin\theta}{\theta} = \frac{\sin(-\theta)}{-\theta}\) y \(\cos\theta=\cos(-\theta)\), la misma desigualdad se cumple para \(\theta < 0\). Esto último nos permite tomar el límite \(\theta\to 0\) sin necesidad de hacerlo por la derecha. Así, $$ \lim_{\theta\to 0} \cos\theta \leq \lim_{\theta\to 0} \frac{\sin\theta}{\theta} \leq \lim_{\theta\to 0} 1 $$ Notando que \(\displaystyle \lim_{\theta\to 0}\cos\theta=1\), por el teorema del sándwich se tiene que $$ \lim_{\theta\to 0} \frac{\sin\theta}{\theta} = 1 \qquad \blacksquare $$ Del que se desprende el siguiente corolario.

Corolario. \(\displaystyle\lim_{x\to 0}\frac{1-\cos x}{x}=0\)

Demostración. $$ \begin{align} \lim_{x\to0}\frac{1-\cos x}{x}\frac{1+\cos x}{1+\cos x} & = \lim_{x\to0} \frac{1-\cos^2 x}{x(1+\cos x)} = \lim_{x\to0}\frac{\sin^2 x}{x(1+\cos x)}\\ & = \lim_{x\to0} \frac{\sin x}{x} \cdot \frac{\sin x}{1+\cos x} = \lim_{x\to0} \frac{\sin x}{x} \cdot \lim_{x\to0} \frac{\sin x}{1+\cos x}\\ & = 1\cdot\frac{\sin (0)}{1+\cos(0)} = \frac{0}{2} = 0 \qquad\blacksquare \end{align} $$

Procederemos a calcular algunos límites trigonométrcos importantes para futuros ejercicios.

1. \(\displaystyle\lim_{x\to0}\frac{\sin 3x}{x}\)
$$ \lim_{x\to0}\frac{\sin 3x}{x}=\lim_{x\to0}\frac{3\sin 3x}{3x}=3\lim_{x\to0}\frac{\sin 3x}{3x} $$ Y haciendo \(u=3x\), nótese que \(u\to 0\) cuando \(x\to 0\). Así, $$ 3 \lim_{u\to0}\frac{\sin u}{u}=3\cdot 1 = \boxed{3} $$
2. \(\displaystyle\lim_{x\to0}\frac{\tan x}{x}\)
$$ \begin{align} \lim_{x\to0}\frac{\tan x}{x} & = \lim_{x\to0}\frac{\frac{\sin x}{\cos x}}{x} = \lim_{x\to0}\frac{1}{\cos x}\cdot\frac{\sin x}{x}\\ & = \lim_{x\to0}\frac{1}{\cos x}\cdot \lim_{x\to0}\frac{\sin x}{x} = \frac{1}{\cos(0)}\cdot 1 = \boxed{1} \end{align} $$
3. \(\displaystyle\lim_{x\to0}\frac{\sin (ax)}{x}\)
$$ \lim_{x\to0} \frac{\sin (ax)}{x} = \lim_{x\to0} \frac{a\sin (ax)}{ax} = a \lim_{x\to0}\frac{\sin (ax)}{ax} $$ Y haciendo \(u=ax\), nótese que \(u\to 0\) cuando \(x\to 0\). Así, $$ a\lim_{u\to0}\frac{\sin u}{u} = a\cdot 1 = \boxed{a} $$
4. \(\displaystyle\lim_{x\to0}\frac{\tan (kx)}{x}\)
$$ \lim_{x\to0} \frac{\tan (kx)}{x} = \lim_{x\to0} \frac{k\tan (kx)}{kx} = k \lim_{x\to0} \frac{\tan (kx)}{kx} $$ Y haciendo \(u = kx\), nótese que \(u\to 0\) cuando \(x\to 0\). Así, $$ k \lim_{x\to0} \frac{\tan (kx)}{kx} = k \lim_{u\to0} \frac{\tan u}{u} = k \cdot 1 = \boxed{k} $$
5. \(\displaystyle\lim_{x\to0}\frac{x}{\sin x}\)
$$ \lim_{x\to0}\frac{x}{\sin x} = \lim_{x\to0} \frac{1}{\frac{\sin x}{x}} = \frac{\lim_{x\to0}1}{\lim_{x\to0} \frac{\sin x}{x}} = \frac{1}{1} = \boxed{1} $$
6. \(\displaystyle\lim_{x\to0}\frac{x}{\sin (\beta x)}\)
$$ \lim_{x\to0}\frac{x}{\sin (\beta x)} = \lim_{x\to0}\frac{1}{\frac{\sin (\beta x)}{x}} = \frac{\displaystyle\lim_{x\to0}1}{\displaystyle\lim_{x\to0}\frac{\sin (\beta x)}{x}} = \boxed{\frac{1}{\beta}} $$

Se resolverán múltiples límites trigonométricos.

Ej.

1. \(\displaystyle\lim_{x\to 0}\frac{\sin 2x+\sin 3x}{\sin 4x+\sin 5x}\)
$$\lim_{x\to 0}\frac{\frac{\sin 2x}{x}+\frac{\sin 3x}{x}}{\frac{\sin 4x}{x}+\frac{\sin 5x}{x}}=\frac{2+3}{4+5}=\boxed{\frac{5}{9}}$$
2. \(\displaystyle\lim_{x\to 0}\frac{x\sec x}{\tan x}\)
$$\lim_{x\to 0}\frac{x\sec x}{\tan x}=\lim_{x\to 0}\frac{x\frac{1}{\cos x}}{\frac{\sin x}{\cos x}}=\lim_{x\to0}\frac{x}{\sin x}=\boxed{1}$$
3. \(\displaystyle\lim_{x\to a}\frac{\sin x-\sin a}{x-a}\)
Sea \(u=x-a\), y obsérvese que \(u\to 0\) cuando \(x\to a\) $$ \begin{align} \lim_{x\to a}\frac{\sin x-\sin a}{x-a} & = \lim_{u\to 0}\frac{\sin(u+a)-\sin a}{u} = \lim_{u\to 0}\frac{\sin u\cos a+\cos u\sin a-\sin a}{u}\\ & = \lim_{u\to 0}\frac{\sin u}{u}\cos a-\frac{1-\cos u}{u}\sin a=\cos a-0\cdot \sin{a} = \boxed{\cos a} \end{align} $$
4. \(\displaystyle\lim_{x\to 0}\frac{\cos x\tan x+\sqrt{1-\cos^2 x}}{x\cos x}\)
$$ \begin{align}\lim_{x\to 0}\frac{\cos x\tan x+\sqrt{1-\cos^2 x}}{x\cos x} &=\lim_{x\to 0}\frac{\tan x}{x}+\frac{\sin x}{x\cos x}=\lim_{x\to 0}\frac{\tan x}{x}+\frac{\tan x}{x}\\ &=\lim_{x\to 0}\frac{2\tan x}{x}=2\lim_{x\to 0}\frac{\tan x}{x}=\boxed{2} \end{align} $$
5. \(\displaystyle\lim_{x\to 0}\frac{\sqrt{1-x}-1}{\sin 4x}\)
$$ \begin{align}\lim_{x\to 0}\frac{\sqrt{1-x}-1}{\sin 4x} & = \lim_{x\to 0}\frac{\sqrt{1-x}-1}{\sin 4x}\cdot\frac{\sqrt{1-x}+1}{\sqrt{1-x}+1} = \lim_{x\to 0}\frac{1-x-1}{\sin 4x}\cdot\frac{1}{\sqrt{1-x}+1} \\ & = \lim_{x\to 0}\frac{-x}{\sin 4x}\cdot\frac{1}{\sqrt{1-x}+1} = -\frac{1}{4}\cdot\frac{1}{2} = \boxed{-\frac{1}{8}} \end{align} $$
6. \(\displaystyle\lim_{x\to 0}\frac{\cos^2 x-1}{\sin x+\sin x\cos x}\)
$$ \begin{align}\lim_{x\to 0}\frac{\cos^2 x-1}{\sin x+\sin x\cos x} &=\lim_{x\to 0}\frac{(\cos x-1)(\cos x +1)}{\sin x(1+\cos x)}=\lim_{x\to 0}\frac{\cos x-1}{\sin x}\\ &=\lim_{x\to 0}-\frac{1-\cos x}{\sin x}=-\lim_{x\to 0}\frac{\frac{1-\cos x}{x}}{\frac{\sin x}{x}}=-\frac{0}{1} =\boxed{0} \end{align} $$
7. \(\displaystyle\lim_{x\to 0}\frac{4\sin^2 x}{x}\)
$$\begin{align}\lim_{x\to 0}\frac{4\sin^2 x}{x}=4\lim_{x\to 0}\frac{\sin x}{x}\sin x = 4\cdot 1\cdot 0=\boxed{0}\end{align}$$
8. \(\displaystyle\lim_{x\to 0}x\csc 6x\)
$$\begin{align}\lim_{x\to 0}x\csc 6x=\lim_{x\to 0}\frac{x}{\sin 6x}\sin x = \boxed{\frac{1}{6}}\end{align}$$