Interpretación de la derivada

Introducción

Hablaremos primero en términos informales, sin dar definiciones explícitas (no hay que preocuparse, las daremos tras la discusión informal).

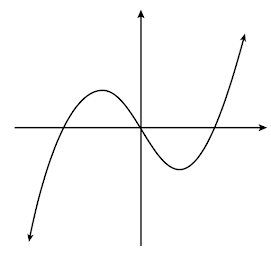
Obsérvese la primera gráfica que se muestra. Esta es la gráfica de una función cúbica impar con dos raíces. La función en sí misma carece de valores máximos y mínimos (que procederemos a llamar máximos y mínimos absolutos), pues los valores de la función se hacen arbitrariamente grandes positivos y grandes negativos a cada lado de la gráfica. No obstante, en la gráfica se pueden observar unos "montes", dentro de los cuales sí se pueden evidenciar un valor máximo y un mínimo (que procederemos a llamar máximos y mínimos locales). Obsérvese que si se restringiera el dominio de la función a un intervalo cerrado \([a,b]\), la función sí alcanzaría un valor máximo y un valor mínimo, pues es continua en todo su dominio (teorema fuerte 3). La función es creciente hasta el primer máximo local y desde el segundo máximo local, y es decreciente entre ellos.

Nótese además que que la gráfica "abre hacia abajo" para valores negativos del dominio, y "abre hacia arriba" para valores positivos. A la dirección en que abre la gráfica le llamamos concavidad. El punto \((0,0)\) es el punto donde se realiza la transición entre ambas aperturas. A este tipo de puntos se les denomina punto de inflexión.

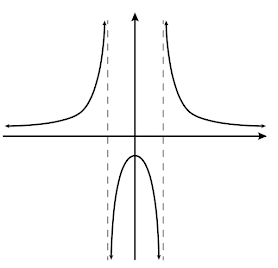
La otra gráfica que se muestra es la de una función racional par con dos asíntotas verticales simétricas y una asíntota horizontal: el eje \(X\). La función tiene un máximo local en \(x=0\), no tiene máximo absoluto y no tiene mínimos. La función es creciente para valores negativos del dominio y es decreciente para valores positivos. Entre las asíntotas se observa que la función es cóncava abajo, y fuera de ellas es cóncava arriba. Como la función no está definida en los cambios de concavidad, tampoco tiene puntos de inflexión.

Este análisis informal podrá parecer sin sentido, pero motiva muchas de las definiciones que seguirán en las secciones subsecuentes.

Máximos y mínimos, parte 1

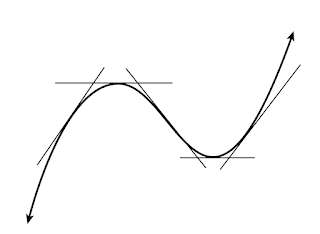
Intuituvamente, se puede ver que una función alcanza un valor máximo o mínimo local cuando la tangente a la gráfica en ese punto es horixontal, i.e. la derivada es cero (ojo: esta condición no es suficiente). A estos puntos con derivada cero les llamaremos puntos críticos, y serán candidatos a máximos y mínimos de una función.

Durante la búsqueda de máximos y mínimos nos debemos asegurar mediante diversos criterios que los puntos críticos son máximos o mínimos. Obsérvese que al tener un máximo local, la tangente a la gráfica pasa de tener pendiente positiva a tener pendiente negativa, y lo contrario ocurre al tratarse de un punto mínimo. A este criterio le llamaremos criterio de la primera derivada.

De esto se desprende que si el cambio en la derivada en un punto crítico es positivo (la derivada es creciente) el punto es mínimo local, y si el cambio es negativo (la derivada es decreciente) el punto es máximo local. De ahí que el otro criterio consiste en analizar el signo de la segunda derivada para determinar la naturaleza del punto. A este criterio le llamaremos criterio de la segunda derivada.

Estos dos criterios nos servirán para dar candidatos, mas no para determinar indudablemente la naturaleza del punto. Procederemos a formalizar todo lo discutido.

Definición. Sea \(f\) una función y \(A\subseteq \text{Dom}(f)\). Un punto \(x\in A\) se dice máximo (mínimo) absoluto de \(f\) sobre \(A\) si \(f(x)\) es mayor o igual (menor o igual) que \(f(y)\) para cualquier \(y\in A\). El número \(f(x)\) recibe el nombre de valor máximo (mínimo) absoluto. A los máximos y mínimos absolutos en conjunto se les llama extremos absolutos.

Teorema.Sea \(f\) una función definida sobre \((a,b)\). Si \(x\) es un extremo absoluto de \(f\) en \((a,b)\) y \(f\) es derivable en \(x\), \(f'(x)=0\).

Demostración. Supóngase que \(x\) es máximo absoluto. Para \(h\in\mathbb{R}\), si \(x+h\in(a,b)\) se tiene que $$f(x)\geq f(x+h)$$ De donde $$f(x+h)-f(x)\leq 0$$ Si \(h > 0\), $$\lim_{h\to 0^+}\frac{f(x+h)-f(x)}{h}\leq 0$$ Si \(h < 0\), $$\lim_{h\to 0^-}\frac{f(x+h)-f(x)}{h}\geq 0$$ Como \(f\) es derivable en \(x\), los límites laterales deben coincidir. Así, \(f'(x)\geq 0\) y \(f'(x)leq 0\), de donde \(f'(x)=0\). \(\blacksquare\)

Definición. Sea \(f\) una función y \(A\subseteq \text{Dom}(f)\). Un punto \(x\in A\) se dice máximo (mínimo) local de \(f\) sobre \(A\) si existe alguna \(\delta > 0\) tal que \(x\) es máximo (mínimo) absoluto de \(f\) sobre \(A\cap (x-\delta,x+\delta)\). El número \(f(x)\) recibe el nombre de valor máximo (mínimo) local. A los máximos y mínimos locales en conjunto se les llama extremos locales.

Teorema. Sea \(f\) una función definida sobre \((a,b)\). Si \(x\) es un extremo local de \(f\) en \((a,b)\) y \(f\) es derivable en \(x\), \(f'(x)=0\).

Demostración. Se sigue del teorema anterior. \(\blacksquare\)

Definición. Se les llama puntos críticos de \(f\) a los valores \(x\in\text{Dom}(f)\) tales que \(f'(x)=0\).

El teorema fuerte 3 nos asegura la existencia de ambos valores extremos absolutos para funciones continuas en intervalos cerrados. Para hallar el valor máximo o mínimo de \(f\) en \([a,b]\) se deben considerar entonces tres clases de puntos:

1. Los puntos críticos de \(f\) en \([a,b]\).
2. Los extremos \(a\) y \(b\).
3. Los puntos \(x\in [a,b]\) tales que \(f\) no es derivable en \(x\).

Ejemplo. Hallar los máximos y mínimos locales de \(f\) definida por \(f(x)=x^3-x\) sobre \([-1,2]\).

Solución. Obtendremos los candidatos. $$f'(x)=3x^2-1$$ $$f'(x)=0\implies 3x^2-1=0\implies x=\pm\frac{1}{\sqrt{3}}$$ Como \(\pm\frac{1}{\sqrt{3}}\in [-1,2]\), ambos puntos son candidatos. La función es derivable en todo el intervalo, por lo que solamente habrá que considerar los extremos \(-1\) y \(2\) además de los puntos críticos. Así, $$f(\tfrac{1}{\sqrt{3}})=-\frac{2}{3}\cdot\frac{1}{\sqrt{3}}$$ $$f(-\tfrac{1}{\sqrt{3}})=\frac{2}{3}\cdot\frac{1}{\sqrt{3}}$$ $$f(-1)=0$$ $$f(2)=6$$ Por lo tanto, el punto mínimo absoluto es \(\tfrac{1}{\sqrt{3}}\) y el punto máximo absoluto es \(2\).

Teoremas notables de derivadas

En esta sección solamente se enunciarán y demostrarán unos cuantos de teoremas de derivadas de gran importancia, algunos relacionados a la sección anterior pero demasiado importantes como para dejar opacarse en ella.

Teorema de Rolle.

Demostración. De la continuidad en \([a,b]\) se tiene que la función tiene un valor mínimo y un valor máximo en \([a,b]\) (teorema fuerte 3). Si el valor máximo o mínimo \(x\) se alcanza en \((a,b)\), por el último teorema de la sección anterior se sigue que \(f'(x)=0\). Si el máximo y mínimo se alcanzan en los extremos, como \(f(a)=f(b)\), se tiene que el máximo y el mínimo coinciden (sean \(\alpha\) y \(\beta\) el máximo y el mínimo, respectivamente). Como \(\beta\leq f(x)\leq \alpha\) para toda \(x\in [a,b]\), se tiene que \(f(x)=\alpha=\beta\) para toda \(x\in [a,b]\). Eso significa que \(f\) es constante en \([a,b]\) y \(f'(x)=0\) para toda \(x\in (a,b)\).

El teorema siguiente es el teorema del valor medio. La interpretación geométrica del teorema del valor medio es muy bella: alguna de las rectas tangentes a la gráfica de una función continua en \([a,b]\) debe tener la misma pendiente que la recta que une a \((a,f(a))\) y \((b,f(b))\). Esto quiere decir que alguna de las tangentes a la gráfica es paralela a la recta que pasa por sus extremos.

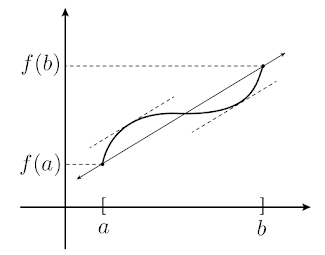
Teorema del valor medio (TVM).

Demostración. Sea \(y:\mathbb{R}\to\mathbb{R}\) definida por $$y(x)=\frac{f(b)-f(a)}{b-a}(x-a)+f(a)$$ Que es la recta por \((a,f(a))\) y \((b,f(b))\). Sea \(h\) la función \(f-y\) dada por $$h(x)=f(x)-\frac{f(b)-f(a)}{b-a}(x-a)-f(a)$$ Nótese que \(h(a)=h(b)=0\). Como \(f\) y \(y\) son ambas continuas en \([a,b]\) y diferenciables en \((a,b)\), \(h=f-y\) también lo es. Por el teorema de Rolle, existe \(x\in(a,b)\) tal que \(h'(x)=0\). Obteniendo \(h'(x)\), $$h'(x)=f'(x)-\frac{f(b)-f(a)}{b-a}$$ De donde $$f'(x)-\frac{f(b)-f(a)}{b-a}=0$$ Y $$f'(x)=\frac{f(b)-f(a)}{b-a}$$ Que es lo que se quería demostrar. \(\blacksquare\)

De estos teoremas se desprenden tres corolarios importantes:

Corolario 1. Si \(f\) está definida en un intervalo \(I\) y \(f'(x)=0\) para toda \(x\) en \(I\), entonces \(f\) es constante sobre \(I\).

Demostración. Por el TVM, como \(f'(x)=0\) para toda \(x\) en \(I\), para cualesquiera \(a,b\in I\) con \(a < b\) se tiene que $$\frac{f(b)-f(a)}{b-a}=0\implies f(b)-f(a)=0\implies f(a)=f(b)$$ Como esto se cumple para cualesquiera \(a,b\in I\), \(f\) es constante en \(I\). \(\blacksquare\)

Corolario 2. Si \(f\) y \(g\) están definidas en un intervalo \(I\) y \(f'(x)=g'(x)\) para toda \(x\) en \(I\), entonces \(f(x)=g(x)+c\) para alguna \(c\in\mathbb{R}\).

Demostración 1. Por el TVM, para \(x,b\in I\) se tiene que $$\frac{f(x)-f(a)}{x-a}=\frac{g(x)-g(a)}{x-a}$$ De donde \(f(x)=g(x)+f(a)-g(a)\), donde \(f(a)-g(a)\in\mathbb{R}\). \(\blacksquare\)

Demostración 2. Como \((f-g)'(x)=f'(x)-g'(x)=0\), el corolario 1 afirma que \(f-g\) es constante en \(I\) y $$f(x)-g(x)=c$$ De donde \(f(x)=g(x)+c\) con \(c\in\mathbb{R}\). \(\blacksquare\)

Corolario 3.

1. \(f'(x) > 0\) para toda \(x\) en \(I\) implica que \(f\) es estrictamente creciente en \(I\).
2. \(f'(x) < 0\) para toda \(x\) en \(I\) implica que \(f\) es estrictamente decreciente en \(I\).

Demostración. Sean \(a,b\in I\) con \(a < b\). Por el TVM, existe \(x\in (a,b)\) tal que $$f'(x)=\frac{f(b)-f(a)}{b-a}$$

1. Si \(f'(x) > 0\) para toda \(x\) en \(I\), como \(b-a > 0\), se obtiene que \(f(b)-f(a) > 0\) y \(f(b) > f(a)\).
2. Si \(f'(x) < 0\) para toda \(x\) en \(I\), como \(b-a > 0\), se obtiene que \(f(b)-f(a) < 0\) y \(f(b) < f(a)\).

Máximos y mínimos, parte 2

Se enunciarán los criterios de la primera y segunda derivada, y se demostrará el segundo.

Criterio de la primera derivada. ea \(c\) un punto crítico de una función \(f\) continua en un intervalo abierto \(I\) que contiene a \(c\). Si \(f\) es derivable en el intervalo, excepto posiblemente en \(c\), entonces \(f(c)\) puede clasificarse como sigue.

1. Si \(f'(x) > 0\) en algún intervalo \((a,c)\) y \(f'(x) < 0\) en algún intervalo \((c,b)\), entonces \(f\) tiene un máximo local en \(c\).
2. Si \(f'(x) < 0\) en algún intervalo \((a,c)\) y \(f'(x) > 0\) en algún intervalo \((c,b)\), entonces \(f\) tiene un mínimo local en \(c\).
3. Si \(f'(x) > 0\) en algún intervalo \((a,b)\) que contiene a \(c\) o \(f'(x) < 0\) en algún intervalo \((a,b)\) que contiene a \(c\), entonces \(c\) no es ni máximo ni mínimo relativo.

Criterio de la segunda derivada. Sea \(f''(c)=0\). Si \(f''(c)>0\) entonces \(c\) es mínimo local de \(f\), si \(f''(c) < 0\) entonces \(c\) es máximo local de \(f\).

Demostración. Por definición, como \(f''(c)=0\), $$f''(c)=\lim_{h\to 0}\frac{f'(c+h)-f'(c)}{h}=\lim_{h\to 0}\frac{f'(c+h)}{h}$$ Si \(f''(c) > 0\), entonces \(\displaystyle\lim_{h\to 0}\frac{f'(c+h)}{h}>0\). Ya se probó que los límites preservan desigualdades, por lo que $$\lim_{h\to 0}\frac{f'(c+h)}{h}>0\implies\frac{f'(c+h)}{h}>0$$ Caso 1. \(h > 0\) Se tiene \(f'(c+h)>0\) para cualquier \(h > 0\), por lo que \(f'(x) > 0\) si \(x\in(c,c+h)\) y \(f\) es creciente en \((c,c+h)\). Caso 2. \(h < 0\) Se tiene \(f'(c+h) < 0\) para cualquier \(h < 0\). Análogamente, \(f\) es decreciente en \((c+h,c)\). Por criterio de la primera derivada, \(c\) es mínimo local de \(f\). El otro caso es análogo. \(\blacksquare\)

Teorema. Supógase que \(f''(c)\) existe. Si \(f\) tiene un mínimo (máximo) local en \(c\), entonces \(f''(c)\geq 0\) (\(f''(c)\leq 0\)).

Demostración. Supóngase por el contrario que \(c\) es mínimo local y \(f''(c) < 0\). Por el criterio de la segunda derivada, \(c\) es máximo local. Como \(c\) es mínimo y máximo, la función es constante em un intervalo que contiene a \(c\), de donde \(f'(c)=0\) y \(f''(c)=0\) ! Por lo que \(f''(c)\geq 0\). \(\blacksquare\)

Concavidad

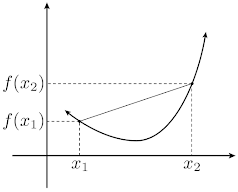
La gráfica de una función \(f\) es cóncava hacia arriba en un intervalo \([a,b]\) si para cualesquiera \(x_1,x_2\in [a,b]\) con \(x_1\not =x_2\) se cumple para toda \(x\in [a,b]\) que $$ f(x) < f(x_1) + \frac{f(x_2)-f(x_1)}{x_2-x_1}(x-x_1) $$ Análogamente, es cóncava hacia abajo si, dadas las mismas hipótesis, se cumple que $$ f(x) > f(x_1) + \frac{f(x_2)-f(x_1)}{x_2-x_1}(x-x_1) $$

Geométricamente, esto significa que la recta que une a cualesquiera dos puntos del intervalo está por encima de la gráfica para funciones cóncavas hacia arriba, y está por debajo para funciones cóncavas hacia abajo.

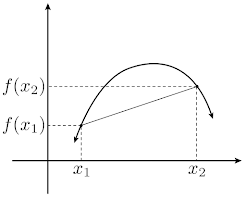
Definición. Un punto \((c,f(c))\) es llamado punto de inflexión de \(f\) si \(f\) es continua en \(c\) y existe un intervalo \([a,b]\) tal que \(f\) es cóncava hacia una dirección en \([a,c]\) y cóncava hacia la otra en \([c,b]\).

Suponiendo que \(f\) es continua en \([a,b]\), un punto \((c,f(c))\) con \(c\in(a,b)\) es de inflexión si ocurre alguna de las siguientes afirmaciones:

1. \(f''(x) > 0\;\forall x\in[a,c]\) y \(f''(x) < 0\;\forall x\in[c,b]\)
2. \(f''(x) < 0\;\forall x\in[a,c]\) y \(f''(x) > 0\;\forall x\in[c,b]\)

Si \(f''(c)\not =0\) en el punto de inflexión, por el criterio de la segunda derivada se tendría que el punto es un máximo o mínimo local y la concavidad se mantendría en una vecindad \((c-\delta,c+\delta)\). Así, es necesario que \(f''(c)=0\) para que \((c,f(c))\) sea punto de inflexión.

Problemas de optimización

Ejemplo.Se quiere construir una caja a partir de un cartón rectangular de \(16\times 25\) cortando cuatro cuadrados de lados iguales, uno en cada esquina. ¿Cuál debe ser el lado de estos cuadrados de tal forma que el volumen de la caja sea mínimo?

Solución. Sea \(x\) el lado del cuadrado. Como se corta \(2x\) de cada lado del cartón, los lados de la base de la caja miden \(16-2x\) y \(25-2x\), y su altura mide \(x\). Puesto que no tiene sentido hablar de lados negativos, es necesario que \(16-2x\geq 0\), de donde \(x\leq 8\). Más aun, no tiene sentido que \(x\) sea negativo. Así, \(x\in[0,8]\). El volumen de la caja está dado entonces por

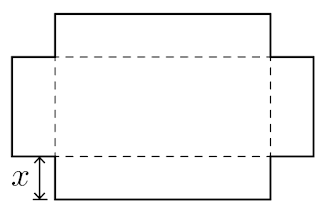
$$V(x)=x(16-2x)(25-2x)=x(4x^2-82x+400)=4x^3-82x^2+400x$$ Que es diferenciable en \(x\in[0,8]\). Derivando e igualando a cero para obtener puntos críticos, $$V'(x)=12x^2-164x+400$$ $$V'(x)=0\implies12x^2-164x+400=0$$ Y por la chicharronera, $$x=\frac{164\pm\sqrt{164^2-4(12)(400)}}{2(12)}=\frac{41\pm\sqrt{481}}{6}$$ Obsérvese que \(\frac{41+\sqrt{481}}{6}>8\), por lo que no es candidato. Así, los candidatos a punto máximo son \(\frac{41-\sqrt{481}}{6}\), \(0\) y \(8\). Evaluando, $$V(0)=0$$ $$V(8)=0$$ $$V(\frac{41-\sqrt{481}}{6})\approx 571.41$$ Por lo que el volumen tiene un valor máximo en \(\boxed{x=\frac{41-\sqrt{481}}{6}}\).

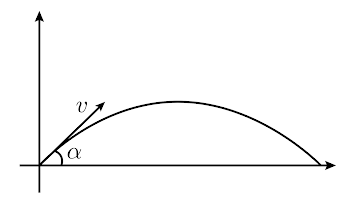
Ejemplo. Una bala de cañón se lanza desde el suelo con velocidad \(v\) y según un ángulo \(\alpha\), de modo que su componente vertical de velocidad es \(v\sin\alpha\) y su componente horizontal es \(v\cos\alpha\). Su distancia \(s(t)\) sobre el nivel del suelo obedece la ley \(s(t)=-4.9t^2+(v\sin\alpha)t\), mientras que su velocidad horizontal permanece constante.

1. Demostrar que la trayectoria de la bala es una parábola.
2. Hallar el ángulo \(\alpha\) que hace máxima la distancia horizontal recorrida por la bala antes de alcanzar el suelo.

Solución.

1. En el instante \(t\), la posición de la bala es \(((v\cos\alpha)t,-4.9t^2+(v\sin\alpha)t)\). Pondremos \(y\) en función de \(x\). Se tiene $$x=(v\cos\alpha)t\implies t=\frac{x}{v\cos\alpha}$$ Sustituyendo en el valor de \(y\), $$ \begin{align}y & = -4.9t^2+(v\sin\alpha)t\\ & = -4.9\left(\frac{x}{v\cos\alpha}\right)^2+(v\sin\alpha)\left(\frac{x}{v\cos\alpha}\right)\\ & = -\frac{4.9}{v^2\cos^2\alpha}x^2+\tan\alpha x \end{align} $$ Y esto último tiene la forma \(ax^2+bx+c\), por lo que es una parábola.
2. Deberemos encontrar la distancia recorrida en función de \(\alpha\). Cuando el valor de \(y\) es cero, la bala no ha sido disparada o bien ya cayó. Hallaremos el tiempo de caída haciendo \(y=0\) y sustituiremos en el valor de \(x\) para hallar la distancia recorrida. Se tiene que $$y=0\implies -4.9t^2+(v\sin\alpha)t=0\implies t(-4.9t+v\sin\alpha)=0$$ Por lo que la altura es cero cuando \(t=0\) (la bala no ha sido disparada) o cuando \(t=\frac{v}{4.9}\sin\alpha\) (la bala ha caído). Sustituyendo esto último en \(x\), se tiene que $$x=(v\cos\alpha)(\frac{v}{4.9}\sin\alpha)$$ $$x=\frac{v^2}{4.9}\sin\alpha\cos\alpha$$ $$x=\frac{v^2}{9.8}\sin(2\alpha)$$ Que es la distancia recorrida en función del ángulo. Nótese que \(\alpha\in[0,\frac{\pi}{2}]\). Derivando e igualando a cero para hallar puntos críticos, $$x'(\alpha)=\frac{v^2}{4.9}\cos(2\alpha)$$ $$x'(\alpha)=0\implies \frac{v^2}{4.9}\cos(2\alpha)=0 \implies \cos(2\alpha)=0$$ Como \(\alpha\in[0,\frac{\pi}{2}]\), el coseno es biyectivo en ese intervalo y tiene función inversa. Se tiene \(2\alpha=\arccos(0)=\frac{\pi}{2}\), de donde \(\alpha=\frac{\pi}{4}\). Los candidatos a máximo son \(0\), \(\frac{\pi}{2}\) y \(\frac{\pi}{4}\). Evaluando, $$x(0)=0$$ $$x(\tfrac{\pi}{2})=0$$ $$x(\tfrac{\pi}{4})=\frac{v^2}{9.8}$$ Por lo que la distancia es máxima para \(\boxed{\alpha=\frac{\pi}{4}}\).

Ejemplo. Se desplaza un ángulo recto a lo largo del diámetro de un círculo de radio \(r\). ¿Qué longitud máxima \(A+B\) puede ser interceptada por el círculo?

Daremos una expresión en coordenadas polares para facilitar la solución. Supóngase que la circunferencia tiene radio \(r\) y centro en el origen. Así, si se traza un radio que forma un ángulo \(\theta\) con el semieje positivo de las \(X\), se tiene que la distancia \(A(\theta)=r\sin\theta\) y la distancia \(B(\theta)=r-r\cos\theta=r(1-\cos\theta)\), por lo que \((A+B)(\theta)=r(1+\sin\theta-\cos\theta)\). Nótese que \(\theta\in[0,\pi]\). Derivando \(A+B\) e igualando a cero para hallar puntos críticos, $$(A+B)'(\theta)=r(\cos\theta+\sin\theta)$$ $$(A+B)'(\theta)=0\implies r(\cos\theta+\sin\theta)=0$$ $$\cos\theta=-\sin\theta$$

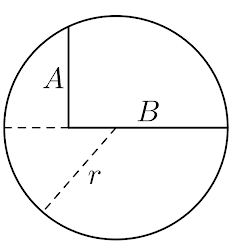
Como \(\theta\in[0,\pi]\), el coseno es biyectivo e invertible. Así, \(\alpha=\frac{3}{4}\pi\), que está cómodamente en el intervalo considerado. Los candidatos entonces son \(0\), \(\pi\) y \(\frac{3}{4}\pi\). Evaluando la función, $$(A+B)(0)=0$$ $$(A+B)(\pi)=2r$$ $$(A+B)(\tfrac{3}{4}\pi)=r(1+\sqrt{2})$$ Por lo que la distancia máxima que se puede interceptar es \(\boxed{A+B=r(1+\sqrt{2})}\).