Continuidad
Tres teoremas fuertes de continuidad
Introducción
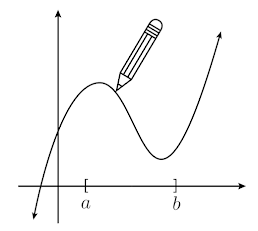
Intuitivamente, podemos entender que una función es continua si su gráfica se puede dibujar sin despegar el lápiz del papel.
Para definir continuidad se puede partir de la idea que, sin importar cuánto se acerque uno a un punto en una función, el
valor de la función en ese punto está determinado por los valores que lo rodean. Si la función tiende a un valor en un punto,
la función tomará ese valor en ese punto. Obsérvese que no siempre se cumple que
Definición. Sea
Se dice que una función que no es continua en un punto determinado es discontinua en dicho punto.
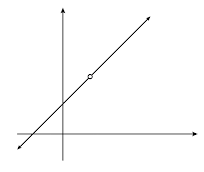
Las discontinuidades que se pueden "cubrir con un punto" son llamadas discontinuidades removibles. Estas se caracterizan
por la existencia de
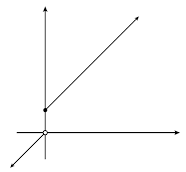
Las discontinuidades en las que los límites laterales existen pero no coinciden son llamadas discontinuidades de salto, pues
la gráfica aparenta "dar un brinco". Para ejemplificar esto, piénsese en el comportamiento en
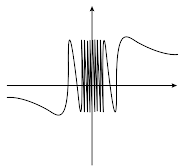
El último tipo de discontinuidad es denominada discontinuidad por oscilación. Esta se ejemplifica muy claramente con el
comportamiento en cero de
Una definición de continuidad mediante
Definición. Una función
Aunque la continuidad es un concepto puntual, también se puede definir sobre intervalos.
Definición. Una función
Definición. Una función
- Es continua en
Puesto que ya se demostró que los límites abren sumas, productos y cocientes, se tiene que
Teorema. Si dos funciones
- Si
Y de la discusión de las funciones polinomiales y racionales de la sección de Límites se obtiene que todas estas funciones son continuas en todo su dominio.
Tres teoremas fuertes de continuidad
En esta sección se presentarán tres teoremas de continuidad de gran importancia. La información que otorgan acerca de las funciones continuas facilita enormemente el análisis de las mismas (tanto gráfico como algebraico). Para los primeros dos teoremas será necesario introducir dos lemas, pero el tercer teorema se seguirá sin mucha dificultad.
Demostración. Se demostrará el caso positivo (el caso negativo es análogo). Sea
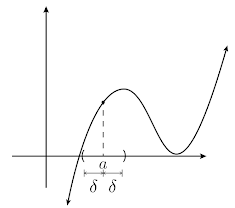
Teorema fuerte 1. Teorema del valor intermedio (1). Sea
Demostración. Sea
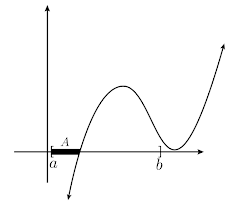
Supóngase que
Lema. Si
Demostración.
Teorema fuerte 2. Si
Demostración. Se demostrará que
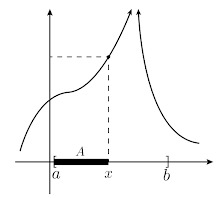
Como
Por lo que
Terminada esta nota, hasta ahora se ha probado que
Teorema fuerte 3. Si
Demostración. Sea
Corolario. Teorema del valor intermedio (2). Sea
Demostración. Sea
Obsérvese que este último teorema es el que justifica la interpretación de la continuidad de una función como la capacidad de dibujar
su gráfica sin despegar el lápiz del papel, pues asegura que la gráfica atraviesa todos los valores en el eje
Para cerrar la sección, se probará un teorema pequeño pero de gran utilidad: el límite conserva desigualdades entre funciones continuas.
Teorema. Sean
Demostración. Como