Problema 22

Analiza la continuidad de la función $f$ en cada uno de los siguientes puntos $x=-1$ y $x=2$. $$ f(x) = \left\{ \begin{array}\\ -x-2 && x < -1 \\ x && -1 < x < 2 \\ 0 && x = -1 \\ 1 && x \geq 2 \end{array} \right.$$

Definición. Se dice que una función $f(x)$ es continua en $x=a$ si y sólo si $ \displaystyle \lim_{x\to a} f(x) = f(a) $

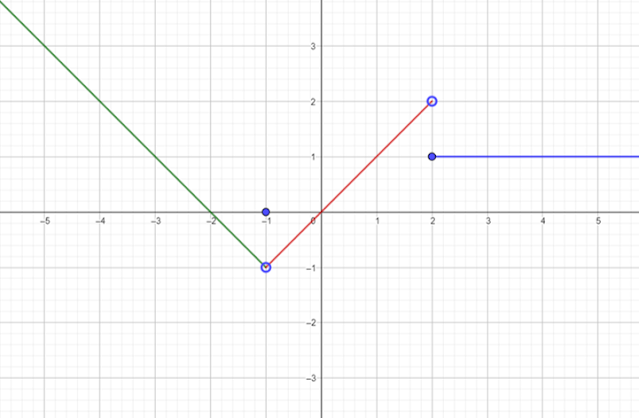
Continuidad de $f$ en $x=-1$: $$ \displaystyle \lim_{x\to -1^+} f(x) = \displaystyle \lim_{x\to -1} x = -1 $$ $$ \displaystyle \lim_{x\to -1^-} f(x) = \displaystyle \lim_{x\to -1} -x-2 = -1 $$ $$ \displaystyle \lim_{x\to -1^+} f(x) = \displaystyle \lim_{x\to -1^-} f(x) \not= f(-1)=0, $$ por lo tanto, $f$ no es continua en $x=-1$. Continuidad de $f$ en $x=2$: $$ \displaystyle \lim_{x\to 2^+} f(x) = \displaystyle \lim_{x\to 2} 1 = 1$$ $$ \displaystyle \lim_{x\to 2^-} f(x) = \displaystyle \lim_{x\to 2} x = 2 $$ $$ \displaystyle \lim_{x\to 2^+} f(x) \not= \displaystyle \lim_{x\to 2^-} f(x) \implies \displaystyle \lim_{x\to 2} f(x) = \nexists, $$ por lo tanto, a pesar de que $f(2)$ existe y es 1, $f$ no es continua en $x=2$.