Problema 34

Una relación que satisface que a cada elemento de su dominio le corresponde uno y sólo un elemento en su contradominio se llama función.

Definiciones fundamentales.

Una función $f: A \rightarrow B$ es inyectiva o uno a uno si y sólo si para cualesquiera $a,b \in A$ con $a \not =b$ se tiene que $f(a) \not = f(b)$, i.e. $ \forall a,b \in A (a \not = b \implies f(a) \not = f(b))$
Una función $f: A \rightarrow B$ es sobreyectiva o sobre si y sólo si para todo $y \in B$ existe $x \in A$ tal que $f(x)=y$, i.e. $\forall y (y \in B \implies \exists x (x \in A \land f(x)=y))$
Una función es biyectiva si y sólo si es inyectiva y sobreyectiva.
Una función es invertible si y sólo si es biyectiva.

En cada uno de los siguientes ejercicios determina si $f: A \rightarrow B$ es o no una función. En caso de serlo demuestra si la función es

Inyectiva
Sobreyectiva
Biyectiva
Invertible

En caso de que existan da las expresiones de $f$ y $f^{-1}$.

P34.A

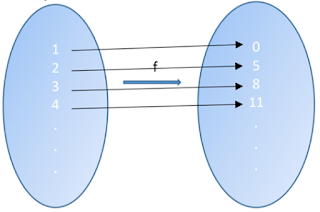
Una posible expresión algebraica para esta función será la siguiente:

$$f: \mathbb{N} \rightarrow \{0\} \cup \{3n-1: n \in \mathbb{N}\}$$ $$f(n)=\left\{\begin{array}\\ 1&& n=0 \\ 3n-1&& n>0 \end{array}\right.$$

Gráfica de la función $f(n)$

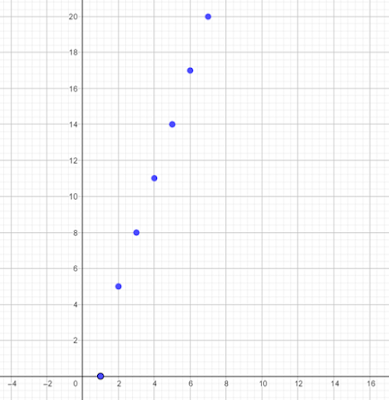
Sí inyectiva, pues para todo par de elementos distintos del dominio, les corresponde un elemento distinto respectivamente en el contradominio.
Sí es sobreyectiva, pues todo elemento del contradominio es imagen de un elemento en el dominio de dicha función.
Por ser inyectiva y sobreyectiva a la vez, es una función biyectiva.
Al tratarse de una función biyectiva, tiene inversa, la cual será de la siguiente forma:

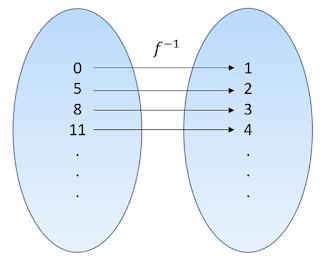
El dominio de $f^{-1}$ será el contradominio de $f$, y el contradominio de $f^{-1}$ será el dominio de $f$. Para obtener la expresión algebraica de la función inversa de $f$, haremos exactamente lo mismo que en el resto de ejercicios: intercambiamos las variables y despejamos a la que antes era la variable independiente, quedándonos de la siguiente manera:

$f^{-1}: \{0\} \cup \{3n-1: n \in \mathbb{N}\} \rightarrow \mathbb{N}$

$$f^{-1}(n)=\left\{\begin{array}\\ 0&& n=1 \\ \frac{n+1}{3}&& n>0 \end{array}\right.$$

Gráfica de la función $f^{-1}(n)$

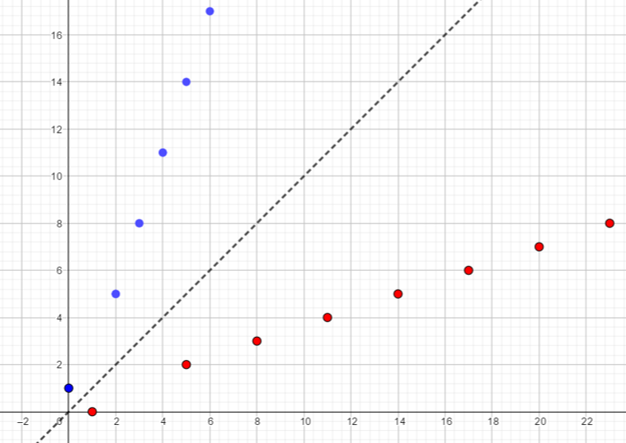
Nótese que una característica de las funciones inversas es que tienen una simetría de reflexión con la función original con respecto a la función identidad $f(x)=x$.

P34.B

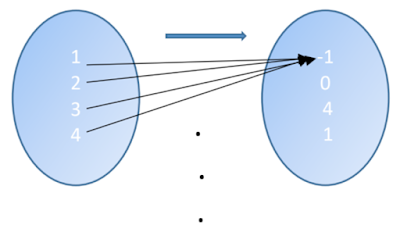
Es una función que no es inyectiva. Supongamos que $Domf=A$, entonces se cumple la negación de que una función sea inyectiva: $\exists 1, 2 \in A (1\not=2 \land f(1)=f(2))$
La función no es sobreyectiva, pues se cumple la negación de que una función sea sobre: $\exists 0 (0 \in B \land \forall x (x \notin A \lor f(x) \not=0))$ Suponiendo que $domf=A$ y su contradominio es el conjunto B.
Como la función no es inyectiva y no es sobre, entonces no es biyectiva.
Al no ser una función biyectiva, no posee inversa.

P34.C

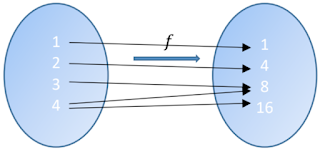
La relación anterior no es una función, pues existe el valor 4 del dominio, y los valores 8 y 16 del contradominio tales que, los pares ordenados $(4, 8)$ y $(4, 16)$ pertenecen a la relación y, sin embargo, $8\not=16$. Todo esto en simbología lógica equivale a lo siguiente:

$ \exists 4 \in A, \exists 8, 16 \in B [((4, 8) \in f \land (4, 16) \in f) \land 4 \not=16]$

Debido a que esta relación no es una función, no será inyectiva, sobre, biyectiva e invertible.

P34.D

$f: A \subset \mathbb{R} \rightarrow B \subset \mathbb{R}$ definida por $f(x)=\frac{x-3}{6x+2}$

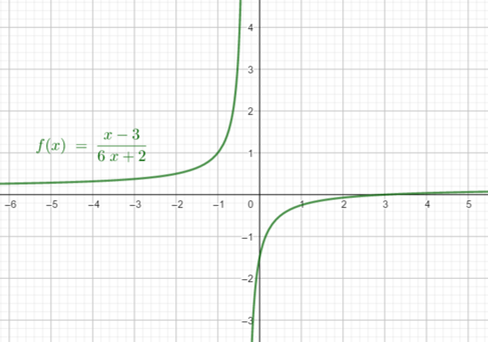
Inyectividad: Supongamos que $f(a)=f(b)$, por demostrar que $a=b$.

Sobreyectividad: Por demostrar que, para todo $y \in B$, existe $x \in A$ tal que $f(x)=y$.

Debido a que $f$ es inyectiva pero no sobreyectiva, entonces no es biyectiva. Sin embargo, esto sucede si la función está definida como $f: \mathbb{R} \rightarrow \mathbb{R}$. Existe una manera de convertir esta función en biyectiva restringiendo su dominio y contradominio. Para ello, restamos al dominio el o los valores en los que la función no está definida; así como restar al contradominio los valores que hacen indefinida la expresión para $x(y)$. Así, para que la función en cuestión sea biyectiva y por ende tenga inversa, la definimos de la siguiente manera:
$f: \mathbb{R}-\{-\frac{1}{3}\} \rightarrow \mathbb{R}-\{\frac{1}{6}\}$
Ya podemos calcular sin preocupaciones la inversa de esta función de la siguiente forma: Si $y=\frac{x-3}{6x+2}$ invertimos las variables obteniendo que $x=\frac{y-3}{6y+2}$ $\implies 6xy+2x=y-3 \implies 6xy-y=-3-2x$ $\implies y(6x-1)=-3-2x \implies y=\frac{-3-2x}{6x-1}$ Nombrando a esta última expresión como la función inversa de $f$, tendremos que $f^{-1}(x)=\frac{-3-2x}{6x-1}$.
El procedimiento de restringir el dominio y contradominio de una función será de mucha utilidad para declararla como biyectiva y así pueda ser invertible. Esta técnica la aplicaremos a los siguientes dos ejercicios desde un comienzo, ya que al tratarse de funciones racionales (con asíntotas horizontales y/o verticales) no serán sobreyectivas cuando están defidas de $\mathbb{R}$ en $\mathbb{R}$; es por ello que redefinimos su dominio y contradominio para calcular su función inversa.

P34.E

$f: A \subset \mathbb{R} \rightarrow B \subset \mathbb{R}$ definida por $f(x)=\frac{x+1}{x^{2}-1}$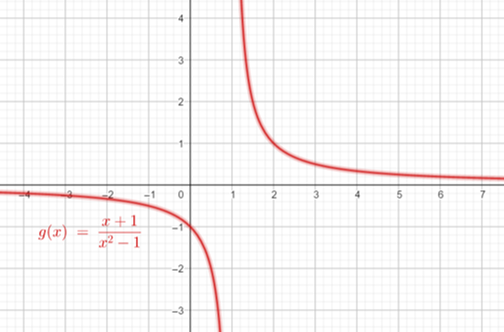

i) Inyectividad: Supongamos que $f(a)=f(b)$, por demostrar que $a=b$. $\frac{a+1}{a^{2}-1}=\frac{b+1}{b^{2}-1} \implies \frac{1}{a-1}=\frac{1}{b-1}$ $\implies a-1=b-1 \therefore a=b$ y $f(x)$ es inyectiva. $\blacksquare$

ii) Sobreyectividad: Por demostrar que, para todo $y \in B$, existe $x \in A$ tal que $f(x)=y$. Si $y=\frac{x+1}{x^{2}-1}=\frac{1}{x-1} \implies y(x-1)=1 \implies xy-y=1$ $\implies xy=1+y \implies x=\frac{1+y}{y}=1+\frac{1}{y}$ De la expresión anterior, tenemos que $y \not=0$ por lo que existe $y=0$ el cual pertenece al contradominio de $f$ y, sin embargo, $f(x) \not=0$. Por lo tanto, $f(x)$ no es sobreyectiva. $\blacksquare$

iii) Redefiniendo la función $f$ de la siguiente manera: $f: \mathbb{R}-\{-1, 1\} \rightarrow \mathbb{R}-\{0\}$ Tendremos que $f(x)$ es inyectiva y sobreyectiva, es decir, biyectiva; y por lo tanto, tiene inversa. Calculando la inversa tendremos lo siguiente: Si $y=\frac{x+1}{x^{2}-1}=\frac{1}{x-1}$ invertimos las variables obteniendo que $x=\frac{1}{y-1}$ $\implies x(y-1)=1 \implies xy-x=1 \implies xy=1+x \implies y=1+\frac{1}{x}$ Nombrando a esta última expresión como la función inversa de $f$, tendremos que $f^{-1}(x)=1+\frac{1}{x}$

P34.F

$f: A \subset \mathbb{R} \rightarrow B \subset \mathbb{R}$ definida por $f(x)=\frac{-2x+5}{3x+1}$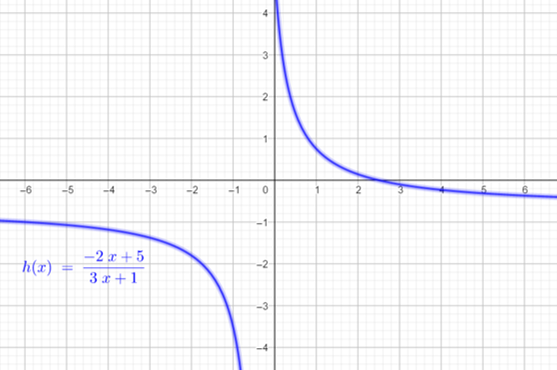

i) Inyectividad: Supongamos que $f(a)=f(b)$, por demostrar que $a=b$. $\frac{-2a+5}{3a+1}=\frac{-2b+5}{3b+1} \implies (-2a+5)(3b+1)=(3a+1)(-2b+5)$ $\implies -6ab-2a+15b+5=-6ab+15a-2b+5 \implies -2a+15b=15a-2b$ $\implies -17a=-17b \therefore a=b$ y $f(x)$ es inyectiva. $\blacksquare$

ii) Sobreyectividad: Por demostrar que, para todo $y \in B$, existe $x \in A$ tal que $f(x)=y$. Si $y=\frac{-2x+5}{3x+1} \implies y(3x+1)=-2x+5 \implies 3xy+y=-2x+5$ $\implies 3xy+2x=5-y \implies x(3y+2)=5-y \implies x=\frac{5-y}{3y+2}$ De la expresión anterior, tenemos que $3y+2 \not=0 \implies y \not=-\frac{2}{3}$ por lo que existe $y=-\frac{2}{3}$ el cual pertenece al contradominio de $f$ y, sin embargo, $f(x) \not=-\frac{2}{3}$. Por lo tanto, $f(x)$ no es sobreyectiva. $\blacksquare$

iii) Redefiniendo la función $f$ de la siguiente manera: $f: \mathbb{R}-\{-\frac{1}{3}\} \rightarrow \mathbb{R}-\{-\frac{2}{3}\}$ Tendremos que $f(x)$ es inyectiva y sobreyectiva, es decir, biyectiva; y por lo tanto, tiene inversa. Calculando la inversa tendremos lo siguiente: Si $y=\frac{-2x+5}{3x+1}$ invirtiendo las variables se tiene que $x=\frac{-2y+5}{3y+1}$ $\implies x(3y+1) = -2y + 5 \implies 3xy + x = -2y + 5$ $ \implies 3xy + 2y = 5 - x \implies y(3x+2)=5-x \implies y = \frac{5-x}{3x+2}$

Nombrando a esta última expresión como la función inversa de $f$, tendremos que $f^{-1}(x)=\frac{5-x}{3x+2}$