Problema 22

Calcula el mínimo, máximo, ínfimo y supremo si es que existe de los siguientes conjuntos.

Para resolver todos los ejercicios, recordaremos las siguientes definiciones fundamentales:
Considérese un conjunto A no vació de números reales.

Un número real $c$ es elemento máximo de A; denotado ello como $c=maxA$, si $\bullet c \in A$ y $\bullet a \leq c$ para todo $a \in A$
Un número real $c$ es elemento mínimo de A; denotado ello como $c=minA$, si $\bullet c \in A$ y $\bullet c \leq a$ para todo $a \in A$
Un número real $c$ es el supremo de A; denotado ello como $c=supA$, si $\bullet c$ es cota superior de $A$ y $\bullet c \leq x$ para toda cota superior $x$ de $A$
Un número real $c$ es el ínfimo de A; denotado ello como $c=infA$, si $\bullet c$ es cota inferior de $A$ y $\bullet x \leq c$ para toda cota inferior $x$ de $A$

P22.A

$A=\{\frac{-1}{n}:n \in \mathbb{N}\}$
Comenzamos visualizando al conjunto como una función cuyo dominio son los números naturales. Obtendremos su gráfica mediante Geogebra de esta y el resto de funciones (mientras sea viable).

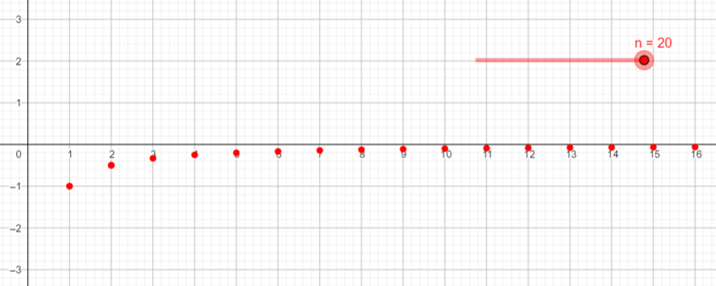
Como -1 es cota inferior del conjunto A y $x \leq -1$ para toda cota inferior $x$ del conjunto, entonces $infA=-1$.
Como $-1 \leq a$ para todo $a \in A$ y $-1 \in A$, entonces $minA=-1$.
Como 0 es cota superior de A y $0 \leq x$ para toda cota superior $x$ de A, entonces $supA=0$.
Como $a \leq 0$ para todo $a \in A$, pero $0 \notin A$, entonces $maxA=\nexists$.

P22.B

$B=\{1+\frac{1}{n}: n \in \mathbb{N}\}$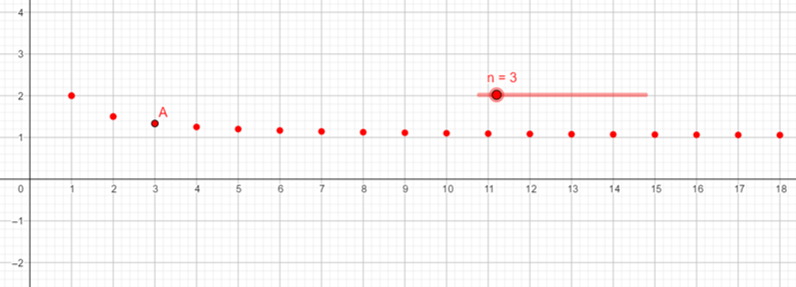

Como 1 es cota inferior del conjunto B y $x \leq 1$ para toda cota inferior $x$ del conjunto, entonces $infB=1$.
Como $1 \leq a$ para todo $a \in B$, pero $1 \notin B$, entonces $minA=\nexists$.
Como 2 es cota superior de B y $2 \leq x$ para toda cota superior $x$ de B, entonces $supA=2$.
Como $a \leq 2$ para todo $a \in B$ y $0 \in B$, entonces $maxB=2$.

P22.C

$C=\{\frac{(-1)^{n}}{n}+n: n \in \mathbb{N}\}$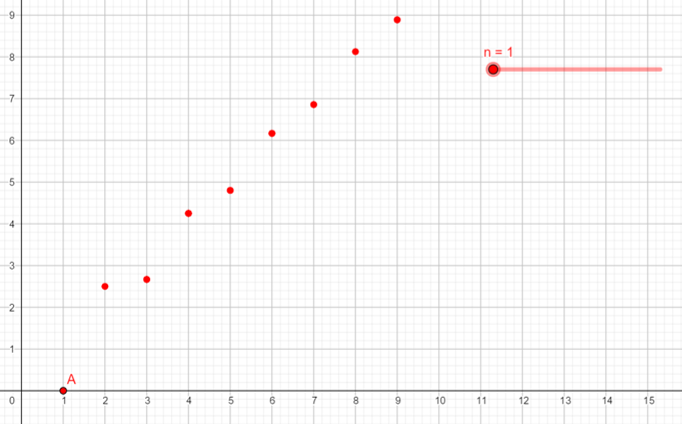

Como se observa, a medida que $n$ aumenta, el valor de la función también lo hace. Así, recurriendo al cálculo de límites de preparatoria, nos daremos cuenta de que el límite cuando $n$ tiende a infinito es igual a infinito; por lo tanto, el conjunto C no tiene supremo y por tanto tampoco máximo, pues no está acotado superiormente.
Como $ 0 $ es cota inferior del conjunto C y $x \leq 0$ para toda cota inferior $x$ del conjunto, entonces $infC = 0$.
Como $0 \leq a$ para todo $a \in C$, y $0 \in C$, entonces $minC=0$.

P22.D

$D=\{(-1)^{n}(\frac{1-n}{n}): n \in \mathbb{N}\}$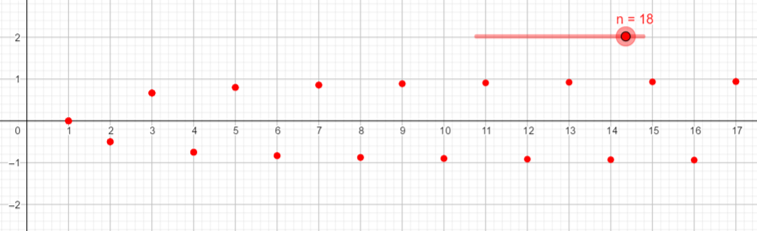

Como $ -1 $ es cota inferior del conjunto D y $x \leq -1$ para toda cota inferior $x$ del conjunto, entonces $infD=-1$.
Como $ 1 $ es cota superior de D y $1 \leq x$ para toda cota superior $x$ de D, entonces $supD=1$.
Tanto el supremo como el ínfimo del conjunto D no pertencen al conjunto, por lo tanto, decimos que no existe un máximo ni un mínimo para este conjunto, pues sus valores oscilan entre $ 1 $ y $ -1 $ cuando $n$ tiende a infinito, sin llegar a tocarlos.

P22.E

$E=\{x \in \mathbb{Q}:x^{2}<2\}$

Este es uno de los conjuntos más famosos para introducir el axioma del supremo para los números reales. Resulta que en los números racionales, este conjunto no está acotado inferior ni superiormente; pues siempre encontramos un racional ya sea positivo o negativo que elevado al cuadrado sea menor que 2. Por ejemplo, veamos el siguiente análisis:

$$0^{2}<2 \checkmark$$ $$1^{2}<2 \checkmark$$ $$(\frac{7}{5})^{2}<2 \checkmark$$ $$(\frac{1393}{985})^{2}<2 \checkmark$$ $$\cdot$$ $$\cdot$$ $$\cdot$$ $$d^{2}<2$$ $$\cdot$$ $$\cdot$$ $$\cdot$$

No hay cota superior mínima (supremo)

$$(\frac{3363}{2378})^{2} > 2$$ $$(\frac{3}{2})^{2} > 2$$ $$2^{2} > 2$$

Es por esto que el conjunto E no posee máximo ni supremo. Y al suceder algo análogo pero con números negativos deducimos que el conjunto no tiene mínimo y tampoco ínfimo.

Aunque este conjunto se haya vuelto un poco aburrido, vale la pena mencionar que la importancia del axioma del supremo radica en que, en los números reales $\mathbb{R}$, dicho conjunto sí tendría supremo e ínfimo, que serían $\sqrt{2}$ y $-\sqrt{2}$, respectivamente; así como máximo y mínimo, que coincidirían con el supremo e ínfimo, respectivamente.

P22.F

$\{n:2^{n} \leq n!, n \in \mathbb{N}\}$

Se puede demostrar mediante Inducción matemática que $2^{n} \leq n!$ para todo $n \in \mathbb{N}$. Lo anterior significa que todos los números naturales complen con dicha propiedad, es decir, tendremos la siguiente equivalencia:

$$\{n:2^{n} \leq n!, n \in \mathbb{N}\}=\mathbb{N}$$

Entonces el conjunto en cuestión es el de los números naturales; el cual no tiene supremo ni máximo, pero sí ínfimo y mínimo, el cual es 1.