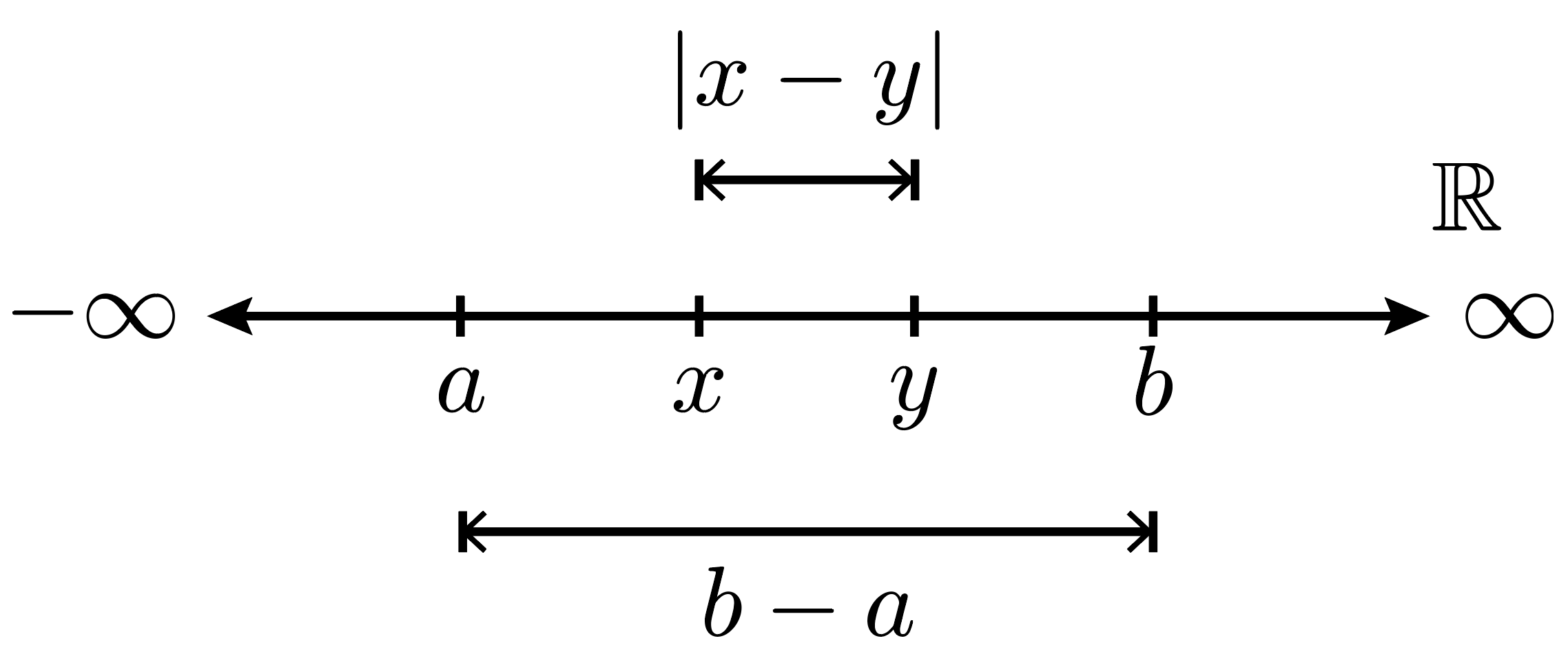Analistas Rifados | Tarea

• Github
• Github
• Github

Problema 17

Si \(a < x < b\) y \(a < y < b\), demostrar que \( \lvert x-y \rvert < b-a\). Interpretar gráficamente el resultado.

---

Demostración

Como \(a < x\) y \(y < b\), se tiene que \(a+y < x+b\), de donde \(a-b < x-y\), o bien \(-(b-a) < x-y\).
Asimismo, como \(x < b\) y \(a < y\), se tiene que \(a+x < y+b\), de donde \(x-y < b-a\). Entonces $$ -(b-a) < x-y < b-a\iff \lvert x-y \rvert < b-a $$ \(\blacksquare\)